(Un)Expected Values: Trying to find EV
Table of Contents
TL;DR:
- I solved the problem of calculating the expected values for predictions.
- The most profitable strategy to date is betting with the positive EV predictions evenly, and that yielded a 240.14% ROI.
Recap of Prior Work
In the previous post, the conclusions were:
| Strategy | ROI |
|---|---|
| Single bets from WTAI where confidence is >=18 | 119.2% |
| Single bets where WTAI and profit agree, with >= 18, 12 confidence respectively. | 60.07% |
| Parlay the shared predictions above. | 80.47% |
Those are all solid returns, but each approach will FEEL different to a user. Many members have reached out to say that they want to see an Expected Value(EV) for each prediction when they are posted so they can better assess whether or not the prediction is worth betting their money on.
This is an approach they have used for some time when betting, on the surface it seemed reasonable, this post walks you through my journey to determine how to present this EV target for them.
What is Expected Value?
Before exploring methods of calculating an EV, gaps, performances, or any of that, I’m going to define a clear and concise definition of what is expected value.
Expected Value (EV) is a measure of the average amount of money you can expect to win or lose per bet placed on a particular wager, Assuming the bet is placed numerous times.
With this, a positive EV would indicate that if you placed a bet at that confidence for a number of times you would have won money overall.
Simple enough, but the rubber meets our road when we now factor in the odds of winning as supplied by our sports book of choice.
A prediction needs to have a confidence score that can drive a probability higher than the odds for the fighter in order to be a positive EV bet.
Calculating EV on WTAI
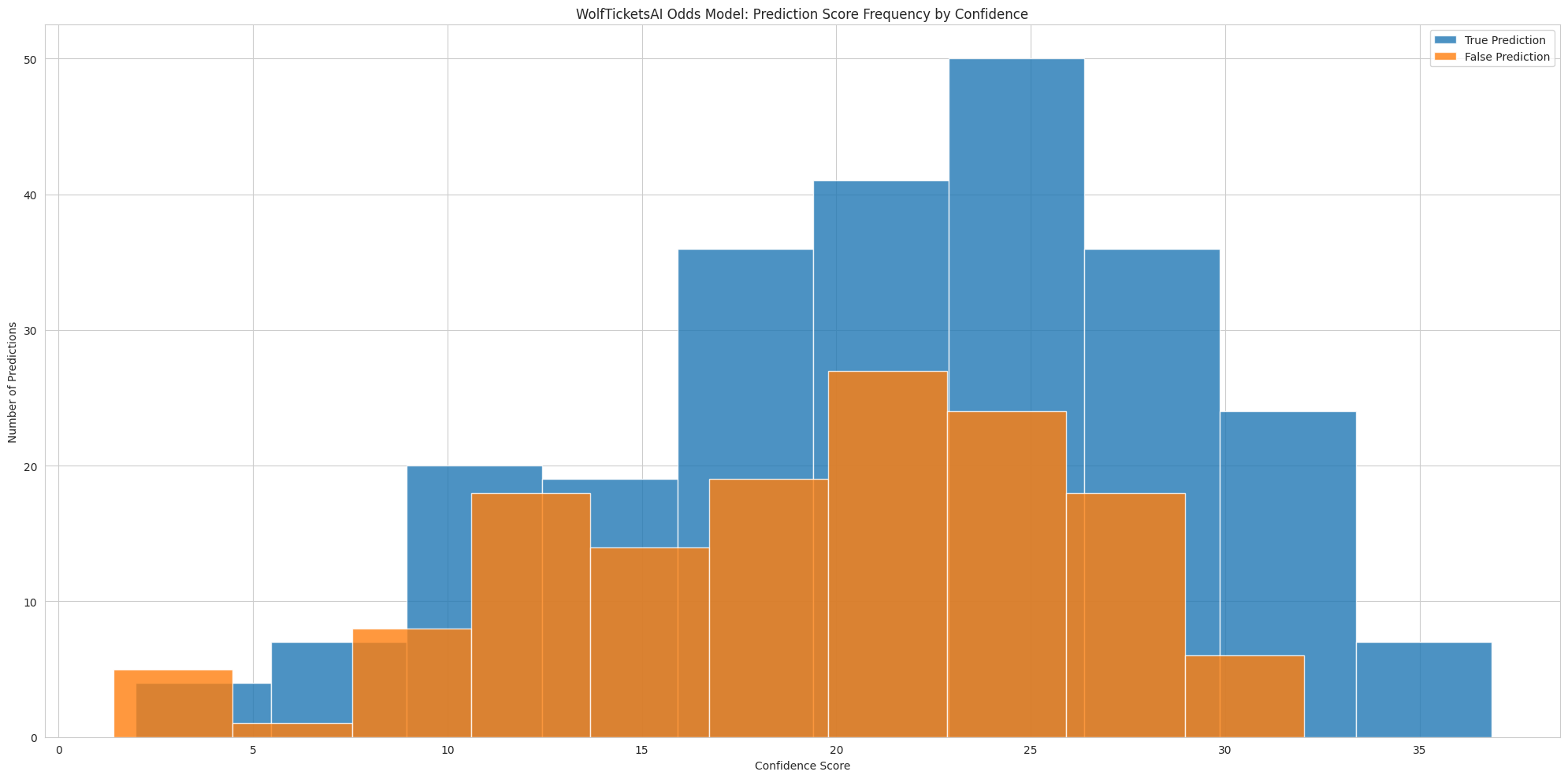
Using the same dataset of WTAI predictions from the previous blog, defining a map between the confidence of a prediction and its average accuracy is pretty simple with Pandas:
1# Load Pandas2import pandas as pd3
4# Load the Dataframe5wtai_df = pd.read_csv("wolfticketsai_data_wtai.csv")6
7# Calculate the percentage of correct predictions by the confidence level (our range)8confidence_correct = wtai_df.groupby('confidence')['correct'].mean() * 1009
10# Define the % we expect the prediction to be correct11wtai_df['percentage_correct_by_confidence'] = wtai_df['confidence'].map(confidence_correct)With that complete I just need to map the odds provided to probabilities, and then take the difference to determine the EV for each prediction.
1# Function to convert American odds to implied probability percentage2def odds_to_probability(odds):3 if odds > 0:4 return 100 / (odds + 100)5 else:6 return -odds / (-odds + 100)7
8# Map it to each prediction9wtai_df['implied_probability'] = wtai_df['odds_prediction'].apply(odds_to_probability) * 10010
11# Calculate the EV12wtai_df['expected_value'] = wtai_df['percentage_correct_by_confidence'] - wtai_df['implied_probability']Fantastic! We have EV and we’re done, time for me to add this to the templates on the site, maybe a specific filter to help call the predictions that work, and to wrap up this blog…
Issues With The EV
The entire dataframe used for this analysis only has 401 total predictions, not nearly the volume needed for proper statistical rigor.

The chart above has been used a few times, but the important thing to note is for most scores there aren’t 100 observations (true or false).
To make it plain to see where the challenges are in using this EV model:
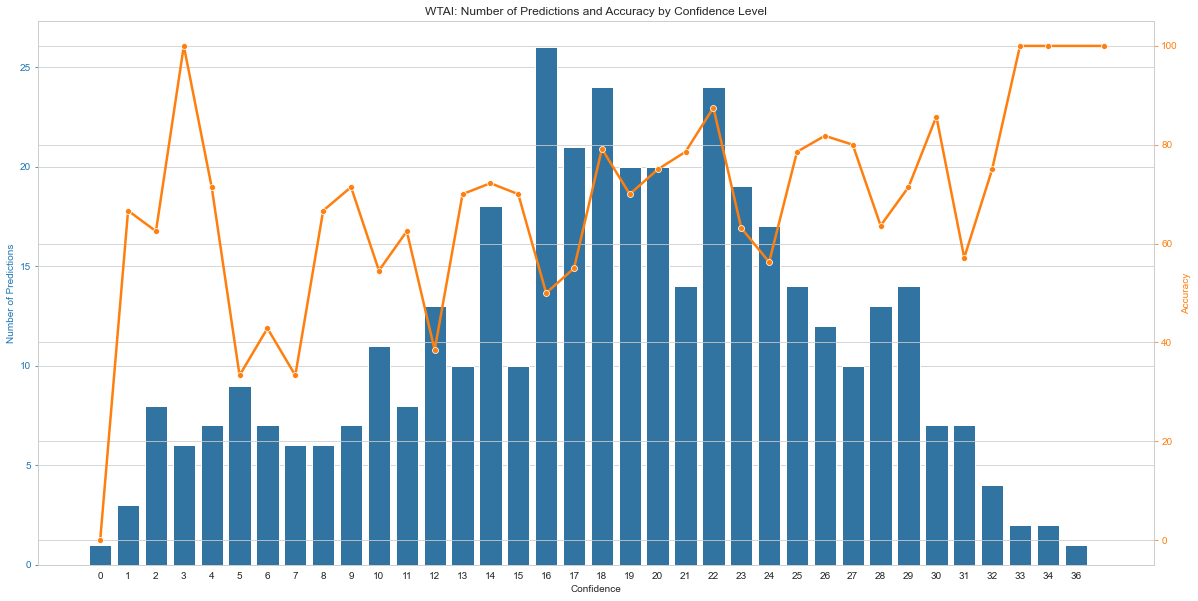
In this plot there’s no relationship with accuracy other than a slight trend upwards on the accuracy as confidence increases. Unfortunately the number of predictions is not uniform, and there’s a lot of volatility.
Is it reasonable to assume that a confidence score of 27 is really that much worse than 22? That seems off, so I need to do a better job of determining the EV.
A Better EV Function
I started by keeping the confidence threshold at 18, it is working really well for single bets without the EV calculation. From there I wanted to know the accuracy average of the predictions with a confidence score of 18 or greater, it worked out to be 77.9% this will be the estimated probability of any prediction scoring 18 or higher going forward.
For the confidence values lower than 18, I kept the average function from the earlier work. With these updated values in place, I recalculated the EV for each prediction and the results were quite promising. We already know that an even bet on the predictions is a very profitable strategy, but can we do better?
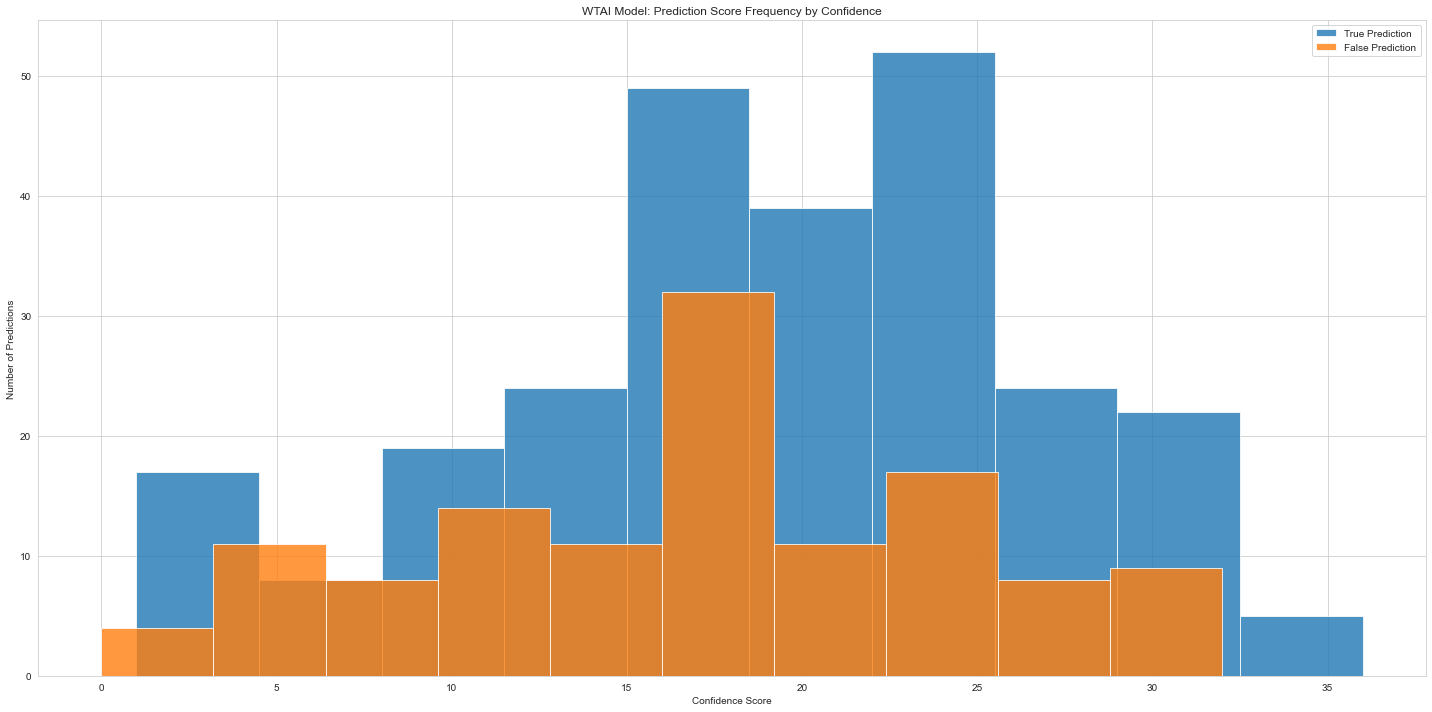
The plot below shows ONLY the specific winnings (payout - bet amount) or losses(-bet amount).
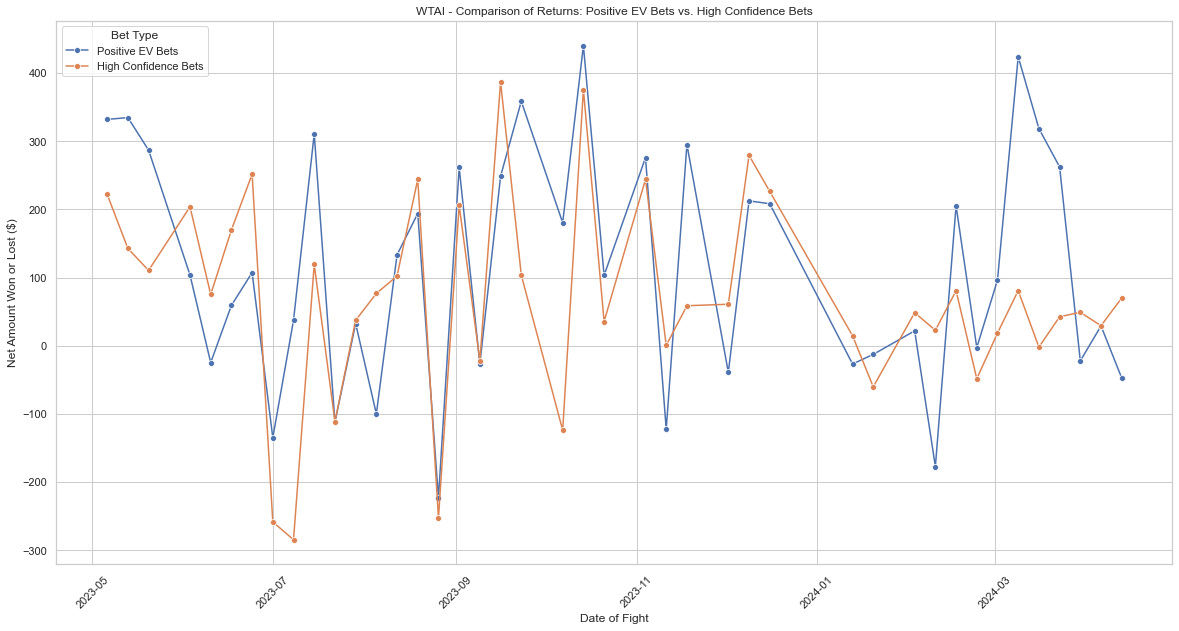
Overall it looks like a positive EV strategy works well in this context, but I wanted to calculate the specific results just to be sure:
1# Calculate totals for each approach2total_wagered_regular = summary_df['total_wagered'].sum()3total_won_or_lost_regular = summary_df['total_won_or_lost'].sum()4
5total_wagered_high_conf = summary_df['total_wagered_high_conf'].sum()6total_won_or_lost_high_conf = summary_df['total_won_or_lost_high_conf'].sum()7print(f"Total wagered on regular bets: ${total_wagered_regular:.2f}")8print(f"Total net amount won or lost from regular bets: ${total_won_or_lost_regular:.2f}")9print(f"Total wagered on high confidence bets: ${total_wagered_high_conf:.2f}")10print(f"Total net amount won or lost from high confidence bets: ${total_won_or_lost_high_conf:.2f}")Yields:
Total wagered on positive EV bets: $7200.00 Total net amount won or lost from positive EV bets: $4802.82
Total wagered on high confidence bets: $5600.00 Total net amount won or lost from high confidence bets: $3027.96
NOT BAD!
Considering we did not include the original bet amounts in either case, both work quite well over an extended period of time, however; THE POSITIVE EV STRATEGY DID WORK BETTER!
This is not a surprise to any of you who have spent a significant amount of time sports betting.
Calculating the total returns into an ROI using the same method as the previous blog post we get an ROI of 240.14% WE HAVE A NEW LEADING APPROACH!
Strategy Breakdown
| Strategy | ROI |
|---|---|
| Single bets from positive EV WTAI predictions | 240.14% |
| Single bets from WTAI where confidence is >=18 | 119.2% |
| Single bets where WTAI and profit agree, with >= 18, 12 confidence respectively. | 60.07% |
| Parlay the shared predictions above. | 80.47% |
What About This Week
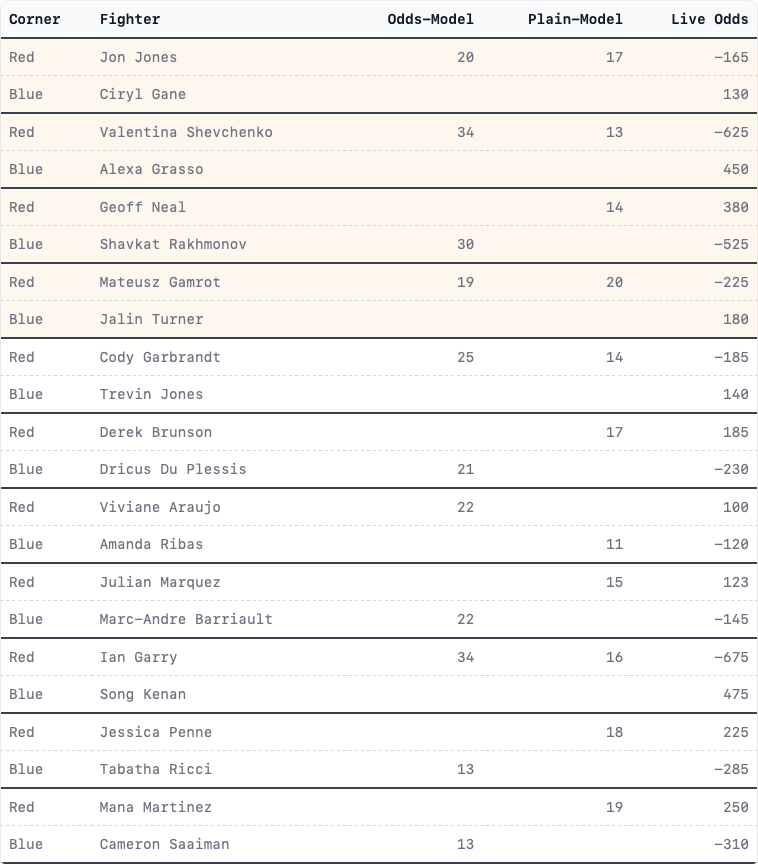
No blog would be complete without calling out how this impacts the current week’s list of fights, so here you go:

It isn’t much, but it’s honest work!
What’s Next
- Embed the EV and positive EV components into the website directly.
- Update betting guidance to follow for positive EV bets.
- Keep listening to members for great ideas to improve WTAI overall!
Good Luck!
-Chris